Projekt edukacyjny - zsbransk.masternet.pl

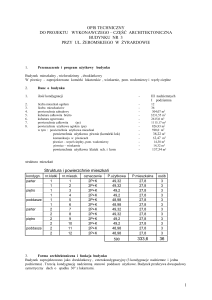
w Gimnazjum w Zespole Szkół
im. Armii Krajowej
w Brańsku
w roku szkolnym 2011/2012
Seria brył
Cele projektu:
-utrwalamy i rozszerzamy wiadomości o bryłach
-co matematycznego powinno łączyć bryły?
-budujemy serie składającą się z trzech brył
Czas realizacji
-semestr pierwszy 2011/2012
Wykonawcy:
Dawid Borowski ,Wojciech Dąbrowski, Karol Gołko, Mateusz
Jakoniuk, Paweł Kamiński, Kacper Malinowski, Anna
Pietrzykowska, Marcin Wiszniewski
Opiekun: Elżbieta Wisłocka
Seria brył
Wielościany
Definicje
Stereometria jest działem geometrii euklidesowej, którego przedmiotem badań są
bryły przestrzenne oraz ich właściwości.
Wielościan
Wielościan- część przestrzeni (bryła) ograniczona ze wszystkich stron wielokątami,
leżącymi w różnych płaszczyznach w taki sposób, że każdy bok jest wspólny dla
dwóch wielokątów wraz z tymi wielokątami.
Wielościan wypukły - wielościan będący bryłą wypukłą, czyli taki, że dowolny
odcinek o końcach w wielościanie zawiera się w nim cały.
Bryłą nie spełniającą tego warunku nazywa się bryłą wklęsłą.
Modele
Graniastosłupem nazywamy taki wielościan, którego dwie
Graniastosłupy
ściany, zwane podstawami, są wielokątami przystającymi
leżącymi na płaszczyznach równoległych, a pozostałe ściany,
zwane ścianami bocznymi, są równoległobokami.
Modele
Opis graniastosłupa
Charakterystyka graniastosłupa n-kątnego
ściana boczna
wierzchołek
krawędź boczna
krawędź podstawy
podstawa
n + 2 ilość ścian (n ścian bocznych i 2 podstawy )
3n
ilość krawędzi (n krawędzi bocznych i 2n krawędzi podstaw )
2n
ilość wierzchołków
Rodzaje graniastosłupów
Graniastosłupy
Proste
Pochyłe
ściany boczne są prostokątami
(są prostopadłe do podstaw)
ściany boczne są równoległobokami
(nie są prostopadłe do podstaw)
Graniastosłupy proste – szczególne przypadki
prostopadłościan
sześcian
– wszystkie jego
ściany są
prostokątami
- wszystkie jego
ściany są kwadratami
Ostrosłupy
Ostrosłupem nazywamy wielościan, którego jedną ze
ścian, zwaną podstawą, jest wielokąt, a pozostałe ściany
są trójkątami posiadającymi jeden wspólny wierzchołek,
zwany wierzchołkiem ostrosłupa. Trójkąty te nazywamy
ścianami bocznymi.
Modele
Charakterystyka ostrosłupa n-kątnego
Opis ostrosłupa
krawędź boczna
krawędź podstawy
wierzchołek
ściana boczna
podstawa
n + 1 ilość ścian (n ścian bocznych i 1 podstawa)
2n
ilość krawędzi (n krawędzi bocznych i n krawędzi podstaw)
n + 1 ilość wierzchołków
Ostrosłupy - szczególne przypadki
Czworościan
- wszystkie jego
ściany są
trójkątami
Czworościan
foremny
- wszystkie jego ściany
są trójkątami
równobocznymi
Rodzaje ostrosłupów
Ostrosłup prawidłowy
jest to ostrosłup, którego podstawą jest wielokąt foremny, a ściany
boczne są jednakowymi trójkątami równoramiennymi
Ostrosłupy
Proste
Pochyłe
Przykłady przekrojów
wielościanów
Przekroje graniastosłupów
Przekroje ostrosłupów
Wielościany niewypukłe
Bryłą nie spełniającą warunku wypukłości nazywa się bryłą wklęsłą.
Przykłady
 ośmiowklęsły ośmiościan
- wklęsły wielościan jednorodny,
powstaje z ośmiościanu foremnego.
 graniastosłup prawidłowy
pięciokątny gwiaździsty
oznaczmy: n liczba krawędzi podstawy
 w graniastosłupie mamy:
 w ostrosłupie mamy:
S=n+2
W=2n
K=3n
wtedy: S + W- K=(n+2)+2n-3n=2
S=n+1
W=n+1
K=2n
wtedy:
S+W- K=(n+1)+(n+1)- 2n =2
np. w graniastosłupie
prawidłowym sześciokątnym
mamy:
S=6+2=8
W=2•6=12
K=3•6=18
wtedy:
S+W-K=9+12-18 = 2
np. w ostrosłupie
prawidłowym sześciokątnym
mamy:
S=6+1=7
W=6 +1= 7
K=2•6=12
wtedy:
S+W-K=7+7-12 = 2
Właściwości
Szczególnymi przykładami wielościanów są wielościany foremne.
Wielościan foremny - wielościan wypukły, którego wszystkie
ściany są przystającymi wielokątami foremnymi i w każdym
wierzchołku zbiega się jednakowa liczba ścian.
Istnieje dokładnie pięć wypukłych wielościanów foremnych. Noszą
one wspólną nazwę brył platońskich.
Modele brył
platońskich
Elementy wielościanów foremnych
czworościan prostopadłościan
foremny
foremny
heksaedr
tetraedrem
S= 4 trójkąty S=6 kwadratów
K= 6
K=12
W= 4
W=8
ośmiościan
foremny
oktaedr
dwunastościan
foremny
dodekaedr
S=8 trójkątów S= 12 pięciokątów
K=12
K=30
W= 6
W=20
dwudziestościan
foremny
ikosaedr
S=20 trójkątów
K= 30
W=12
Dlaczego „bryły platońskie”
 To właśnie Platon wyobrażał sobie, że wszechświat
tworzą cztery elementy: ogień, ziemia, woda i
powietrze, a każda z tych żywiołów zbudowany jest z
cząsteczek, które mają kształt wielościanów
foremnych. U Platona cząsteczki ognia mają kształt
czworościanów, sześcian symbolizował ziemię,
ośmiościan symbolizował powietrze, dwudziestościan
symbolizował wodę, dwunastościan miał
symbolizować eter (wg filozofów była to substancja
Źródło:http://gnosis.art.pl
wypełniająca cały wszechświat).
 W starożytności bryłom tym przypisywano też pięć znanych
wówczas planet : czworościan był uosobieniem planety Jowisz,
sześcian- Saturn, ośmiościan – Merkury, dwunastościan - Mars,
dwudziestościan - Wenus. - stąd do dziś nazwa "wielościany
kosmiczne".
 W XVII wieku Kepler użył wielościanów foremnych do swojego
modelu kosmologicznego - układu słonecznego. Bryły te były
umieszczone wewnątrz sfery reprezentującej orbitę Saturna.
Źródło:http://en.wikipedia.org/
 Dziś już dzięki Euklidesowi możemy dowieść, że
jest ich dokładnie pięć.
Dlaczego wielościanów
foremnych jest tylko 5
O liczbie wielościanów foremnych możemy przekonać się z twierdzenia Eulera.
Oznaczmy:
W - ilość wszystkich wierzchołków wielościanu, W ≥ 4,
K - ilość jego wszystkich krawędzi, K ≥ 6,
S - ilość ścian, S ≥ 4
p = ilość krawędzi w jednej ścianie, , p ≥ 3,
q = ilość krawędzi przy jednym wierzchołku q ≥ 3. .
Każda krawędź należy do dwóch ścian i łączy dwa wierzchołki. Stąd więc
wynikają dwie zależności:
Sp=2K
qW=2K
Stąd :
S= 2K/p,
W = 2K/q,
podstawiając do równania Eulera S + W - K = 2 dla wielościanów daje
zależność: 2K/q +2K/p - K = 2 , która po podzieleniu stronami przez 2K daje
równanie: 1/p +1/q= 1/2+ 1/K
Ono oznacza, że 1/p + 1/q > 1/2. Ten związek nie spełniają dowolne liczby
naturalne p i q. Wybierając wszystkie pary p ≥ 3,q ≥ 3 otrzymujemy tylko pary:
(3,3), (3,4), (4,3), (3,5) i (5,3). Dla p ≥ 6 lub q ≥ 6 związek ten już nie zachodzi.
Podstawiając wyznaczone pary liczb (p,q) do wzorów na W, S i K otrzymujemy
wartości określające pięć wielościanów foremnych
WNIOSKI
liczbami ścian wielościanu foremnego mogą być tylko liczby 4, 6, 8,
12, 20.
jedynymi wielokątami foremnymi, które mogą być ścianami brył
foremnych są te dla których liczba boków b {3, 4, 5}.
3 jest najmniejszą liczbą, dla której mamy wielokąt,
dla b = 6 nie jesteśmy już w stanie uzyskać bryły. Sześciokąt
foremny ma kąt wewnętrzny 120, a skoro w dowolnym wierzchołku
bryły spotkać się muszą co najmniej z = 3 ściany, gdyż 120 × 3 = 360.
dla b = 4, 5 w jednym wierzchołku mogą się spotkać jedynie z = 3
ściany,
dla b = 3 mogą się spotkać 3, 4, 5 ściany, czyli z  {3, 4, 5}.
w × z = b × s
2k = b × s, podstawiając te wyniki do wzoru Eulera dostajemy :
s = s(b, z) = 4z/ 2z + 2b − bz
rozważając wszystkie przypadki mamy:
s(3, 3) = 4
s(4, 3) = 6
s(3, 4) = 8
s(3, 5) = 20
s(5, 3) = 12
.
Bryły platońskie (ze ścianami i bez ścian) narysowane przez
Leonarda da Vinci do książki Luca Pacioli pt. Boska proporcja (1509r)
 ośmiościan
dwunastościan
 czworościan
 sześcian
 dwudziestościan
 Studium fontanny Loenarda
Da Vinci (w środku m.in.
czworościan wpisany w
sześcian)
 Dwunastościan na obrazie "Ostatnia
wieczerza" Salvadora Dali.
Leonardo Da Vinci - Sześciany
Dwunastościan gwiaździsty mały
znajduje się na posadzce bazyliki
św. Marka w Wenecji –autor Paolo
Uccello
Nagrodzony Noblem trójwymiarowy
model struktury atomowej węgla C60
składający się ze ścian pięcio- i
sześciokątnych
Ciekawostki
 Kilkadziesiąt lat temu znaleziono na terenie Szkocji bryły wykonane z
kamienia, które do złudzenia przypominają platońskie bryły. Ich wiek datuje
się na co najmniej 3 tys. lat. Są więc starsze od Platona (428-348 p.n.e.) o
co najmniej o 500 lat... Kamienne bryły znajdują się w "Ashmolean
Museum", w Oxford w Anglii. Oto one:
 Dwunastościan i dwudziestościan z brązu z czasów rzymskich, których
przeznaczenie nie jest znane.
Pszczeli sekret
Pszczoły poza tym, iż są bardzo
pracowite, mają też ogromną
wiedzę matematyczną. Pszczoły
budują z wosku komórki w kształcie
prawidłowych graniastosłupów
sześciokątnych. Graniastosłupy
takie nie tylko szczelnie wypełniają
przestrzeń, tworząc
charakterystyczny "plaster miodu",
ale jednocześnie zużywają
najmniejszą ilość budulca.
Kształty kryształów
Struktura hydratu metanu
Kryształ hexagonalny
Kryształ soli kuchennej
Piłka futbolowa
Piłka futbolowa uszyta jest z wielokątów. Gdyby nie elastyczność materiału, z
którego jest wykonana, byłaby wielościanem - dwudziestościanem ściętym.
Dwudziestościan ścięty to wielościan półforemny o 32 ścianach w kształcie 20
sześciokątów foremnych i 12 pięciokątów foremnych. Posiada 90 krawędzi i 60
wierzchołków.
Wzór Eulera
podana w tw. Eulera
S + W - K= 2
równość zachodzi.
32 + 60 - 90 = 2
Tangram – chińska gra znana od ok. 3000
lat. Tangram to kwadrat, który składa się z
7 części (tan):
Stożek
Kula
Walce
Podsumowanie
-Nauczyliśmy się rozpoznawać różne
bryły (graniastosłupy, ostrosłupy, bryły
obrotowe, wielościany platońskie).
-Potrafimy rysować i sklejać siatki tych
brył.
-Umiemy składać nasze modele w
serie brył.
-Do tej pory o niektórych bryłach nie
uczyliśmy się jeszcze na lekcjach
matematyki
Bibliografia
• Matematyka dla klas I, II, III Gim.- podręcznik GWO.
• Matematyka w Szkole- nr. 17 listopad-grudzień 2002r.
• Internet: Wikipedia