Wykład 27 Elementy współczesnej fizyki atomów i cząsteczek. ( )

Wykłady z fizyki – Piotr Posmykiewicz
1
Wykład 27
Elementy współczesnej fizyki atomów i cząsteczek.
12.1 Atom wodoru w mechanice kwantowej.
Znalezienie poziomów energetycznych elektronu w atomie wodoru (a także układów
wodoropodobnych: jonu helu He+, dwukrotnie zjonizowanego litu Li++ i innych) sprowadza
się do problemu ruchu elektronu w kulombowskim polu jądra.
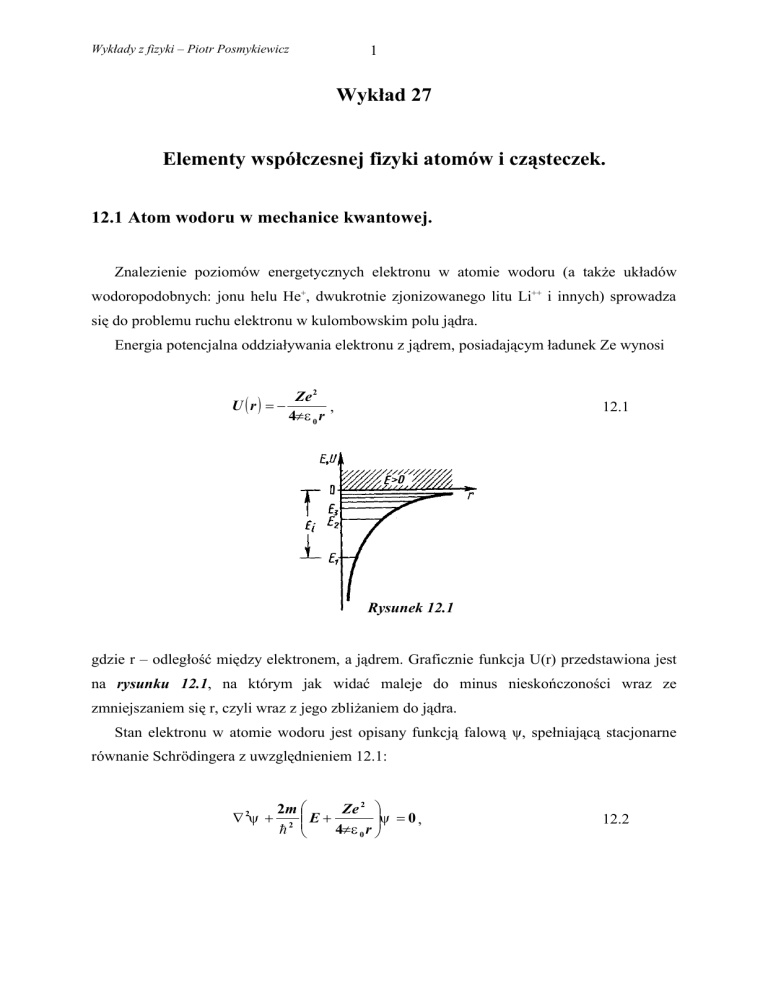
Energia potencjalna oddziaływania elektronu z jądrem, posiadającym ładunek Ze wynosi
U (r) = −
Ze 2
,
4πε 0 r
12.1
Rysunek 12.1
gdzie r – odległość między elektronem, a jądrem. Graficznie funkcja U(r) przedstawiona jest
na rysunku 12.1, na którym jak widać maleje do minus nieskończoności wraz ze
zmniejszaniem się r, czyli wraz z jego zbliżaniem do jądra.
Stan elektronu w atomie wodoru jest opisany funkcją falową ψ, spełniającą stacjonarne
równanie Schrödingera z uwzględnieniem 12.1:
∇ 2ψ +
2m 
Ze 2 

ψ = 0 ,
E
+
 2 
4πε 0 r 
12.2
Wykłady z fizyki – Piotr Posmykiewicz
2
gdzie E – energia całkowita elektronu w atomie. Ponieważ pole, w którym porusza się
elektron jest polem centralnym, to aby rozwiązać powyższe równanie zwykle wprowadza się
sferyczny układ współrzędnych: r, υ, φ. Nie będziemy analitycznie rozwiązywać tego
równania różniczkowego, a jedynie ograniczymy się do rozpatrzenia najważniejszych
wniosków, które z niego wynikają.
1. Energia. W teorii równań różniczkowych udowadnia się, że równania typu 12.2 mają
rozwiązania spełniające warunek jednoznaczności, skończoności i ciągłości funkcji falowej
ψ, tylko dla energii własnych przyjmujących wartości:
En = −
1 Z 2 me 4
n 2 8h 2 ε 02
(n = 1, 2, 3, ...),
12.3
tzn. dla ujemnego dyskretnego zbioru wartości energii własnych.
W ten sposób, tak jak w przypadku nieskończenie głębokiej jamy potencjału i oscylatora
harmonicznego, rozwiązanie równania Schrödingera dla atomu wodoru prowadzi do
pojawienia się dyskretnych poziomów energetycznych. Dozwolone wartości E1, E2, E3, ...
przedstawione są na rysunku 12.1 w postaci poziomych prostych. Najniższy poziom E1
odpowiada najmniejszej energii całkowitej i nazywa się podstawowym, wszystkie pozostałe
poziomy (En > E1, n = 2, 3, ...) nazywają się wzbudzonymi. Jeżeli E < 0 to ruch elektronu jest
związany – znajduje się wewnątrz hiperbolicznej jamy potencjału. Z rysunku wynika, że w
miarę wzrostu głównej liczby kwantowej n poziomy energetyczne położone są coraz gęściej i
dla n = ∞ , E ∞ = 0 . Dla E > 0 ruch elektronu nazywamy swobodnym – może on oddalić się
na nieskończoną odległość; obszar ciągłego widma E > 0 (część zakreskowana na rysunku)
odpowiada atomowi zjonizowanemu. Energia jonizacji dla atomu wodoru jest równa
E i = − E1 =
me 4
= 13,55eV .
2 2
8h ε 0
Wzór 12.3 pokrywa się ze wzorem otrzymanym przez Bohra (patrz wykład poprzedni).
Jednak Bohr musiał wprowadzać dodatkowe postulaty, gdy tymczasem w mechanice
kwantowej dyskretne wartości energii będąc wynikiem samej teorii, wynikają bezpośrednio z
rozwiązania równania Schrödingera.
Wykłady z fizyki – Piotr Posmykiewicz
3
2. Liczby kwantowe. W mechanice kwantowej udowadnia się, że równanie Schrödingera
spełniają funkcje własne ψ nlml ( r ,ϑ ,ϕ ) określone poprzez trzy liczby kwantowe: główną
liczbę kwantową n, orbitalną l i magnetyczną ml.
Główna liczba kwantowa n, zgodnie z 12.3, określa poziomy energetyczne elektronu w
atomie i może przybierać dowolne całkowite wartości:
n = 1,2,3,...
Z rozwiązania równania Schrödingera wynika, że moment pędu (inaczej orbitalny moment
pędu) elektronu jest skwantowany, tzn. nie może mieć wartości dowolnych, a jedynie
określone wzorem
Ll =  l ( l + 1) ,
12.4
gdzie l – orbitalna liczba kwantowa, które dla danego n może przyjmować wartości
l = 0,1,2,..., ( n − 1) ,
12.5
tzn. n wartości i określa moment pędu elektronu w atomie.
Z rozwiązania równania Schrödingera wynika także, że wektor Ll momentu pędu może
mieć tylko takie orientacje w przestrzeni, dla których jego rzut Llz na kierunek z zewnętrznego
pola magnetycznego przybiera wartości kwantowe będące wielokrotnością  :
Llz = m l ,
12.6
gdzie ml – magnetyczna liczba kwantowa, wartości której, przy danym l, mogą być:
m l = − l ,− l + 1,...,−1,0,+1,..., l − 1, l ,
12.7
czyli 2l+1 wartości. W ten sposób, magnetyczna liczba kwantowa określa rzut wektora
momentu pędu elektronu na zadany kierunek, przy czym wektor momentu pędu elektronu
w atomie może mieć 2l+1 wartości.
Wykłady z fizyki – Piotr Posmykiewicz
4
Obecność magnetycznej liczby kwantowej ml powinno prowadzić do rozszczepienia w
polu magnetycznym poziomu energetycznego o głównej liczbie kwantowej n na 2l+1
podpoziomów. W związku z tym w widmie atomu powinno się obserwować się
rozszczepienie linii widmowych. Rzeczywiście rozszczepienie linii widmowych w
zewnętrznym polu magnetycznym zostało odkryte przez fizyka holenderskiego P. Zeemana i
nosi nazwę zjawiska Zeemana. Rozszczepienie poziomów energetycznych w zewnętrznym
polu elektrycznym także zostało odkryte doświadczalnie i nosi nazwę zjawiska Starka.
Pomimo, iż energia elektronu zależy tylko od głównej liczby kwantowej n, to każdej
wartości własnej En (oprócz E1) odpowiada kilka funkcji własnych ψ nlml różniących się
wartościami l i ml. W rezultacie atom wodoru może mieć jedną i tę samą wartość energii
znajdując się w kilku różnych stanach. Ponieważ dla danego n orbitalna liczba kwantowa l
może zmieniać się od 0 do n – 1, a każdej wartości l odpowiada 2l +1 różnych wartości ml, to
liczba różnych stanów odpowiadających danemu n jest równa
n−1
∑ ( 2 l + 1) = n
2
.
12.8
l =0
Stany o jednakowych energiach nazywamy stanami zdegenerowanymi lub zwyrodniałymi,
a liczbę stanów o jednakowej energii nazywamy krotnością degradacji.
Rysunek 12.2
Wykłady z fizyki – Piotr Posmykiewicz
5
Prawdopodobieństwo znalezienia elektronu w różnych miejscach atomu jest różne. Elektron
w trakcie swojego ruchu jest jak gdyby „rozmazany” w całej objętości, tworząc jak gdyby
obłok
(chmurę)
elektronowy,
znalezienia elektronu w
którego
gęstość
charakteryzuje
prawdopodobieństwo
różnych punktach objętości atomu. W mechanice kwantowej
przyjmuje się, że liczby kwantowe n i l charakteryzują rozmiar i kształt obłoku
elektronowego, a liczba kwantowa ml charakteryzuje zorientowanie obłoku w
przestrzeni.
W fizyce atomowej, przez analogię ze spektroskopią, stan elektronu opisany liczbą l = 0
nazywa się stanem s, stan opisany l = 1 – stanem p, l = 2 – stanem d, l = 3 – stanem f itd.
Wartość głównej liczby kwantowej n umieszczana jest przed powyższymi oznaczeniami
literowymi. Na przykład, elektrony w stanach z n = 2 i l = 0 i 1 zaznacza się odpowiednio jako
2s i 2p.
Na rysunku 12.2, jako przykład przedstawiono kształt chmury elektronowej dla
2
przypadku n = 1 i n = 2 pokazujące wartość wyrażenia ψ nlml .
3. Widmo. Liczby kwantowe n, l i ml pozwalają na bardziej pełny opis widma
atomowego niż to miało miejsce w przypadku teorii Bohra.
W mechanice kwantowej pojawiają się tzw. reguły wyboru, ograniczające ilość
możliwych przejść elektronów w atomie związanych z emisją i pochłanianiem światła.
Udowodniono teoretycznie i doświadczalnie, że w przypadku dipolowego promieniowania
elektronu, poruszającego się w centralnym i symetrycznym polu jądra atomowego możliwe są
tylko takie przejścia, dla których: 1) zmiana orbitalnej liczby kwantowej spełnia warunek
∆l = ±1
12.9
2) zmiana magnetycznej liczby kwantowej spełnia warunek
∆ m l = 0, ± 1 .
Dla widm optycznych zasady wyboru są praktycznie spełnione. W zasadzie jednak
możliwa obserwacja słabych „zabronionych” linii, powstających na przykład podczas przejść
ze zmianą ∆l = 2 . Pojawienie się takich linii wyjaśnia się tym, że ścisła teoria, zakazując
przejścia dipolowe, pozwala na przejścia odpowiadające promieniowaniu wysyłanemu przez
bardziej złożone układy ładunków, np. kwadrupole. Prawdopodobieństwo przejść
Wykłady z fizyki – Piotr Posmykiewicz
6
kwadrupolowych (przejścia z ∆l = 2 ) jest jednak znacznie mniejsze niż prawdopodobieństwo
przejść dipolowych, dlatego linie „zabronione” są znacznie słabsze.
E,eV
Seria Lymana
Seria Balmera
Rysunek 12.3
Uwzględniając liczbę wszystkich możliwych stanów, odpowiadających danemu n i regułę
wyboru 12.9 rozpatrzmy linie widmowe w atomie wodoru (Rysunek 12.3):
Dla serii Lymana istnieją przejścia
np → 1s
(n = 1, 2, 3, ...)
Dla serii Balmera
np → 2 s , ns → 2 p , nd → 2 p (n 3, 4, ...)
itd.
Przejście elektronu ze stanu podstawowego do wzbudzonego związane jest ze
zwiększeniem energii atomu i może zachodzić tylko podczas dostarczania energii atomu z
zewnątrz, np. w wyniku pochłonięcia przez atom fotonu. Ponieważ pochłaniający energię
atom znajduje się na ogół w stanie podstawowym, to widmo atomu wodoru powinno składać
się z linii odpowiadającym przejściom 1s → np (n = 2, 3, ...), co jest całkowicie zgodne z
doświadczeniem.
12.2 Stan elektronu -1s w atomie wodoru.
Stan 1s elektronu w atomie wodoru jest stanem o symetrii sferycznej, tzn. nie zależy od
kątów ϑ i ϕ . Funkcja falowa ψ elektronu w tym stanie określona jest tylko przez odległość r
elektronu od jądra, tzn. ψ = ψ 100 ( r ) , gdzie cyfry 100 pokazują odpowiednio, że n = 1, l = 0, ml
Wykłady z fizyki – Piotr Posmykiewicz
7
= 0. Równaniu Schrödingera dla stanu 1s elektronu w atomie wodoru odpowiada funkcja w
postaci
ψ = Ce − r / a
2
(
gdzie a =  4πε 0 / me 2
)
12.10
- wielkość pokrywająca się z pierwszym promieniem Bohra w
atomie wodoru, C – pewna stała określona przez warunek normalizacji.
Dzięki symetrii sferycznej funkcji ψ prawdopodobieństwo znalezienia elektronu w
odległości r jest takie samo we wszystkich kierunkach. Dlatego też, element objętości dV,
odpowiadający jednakowej gęstości prawdopodobieństwa, zwykle jest przedstawiony w
postaci objętości warstwy kulistej o promieniu r i grubości dr: dV = 4πr2dr. Wtedy, zgodnie z
warunkiem normalizacji i 12.10
∞
2
∞
1 = ∫ ψ dV = ∫ C 2e −2 r / a 4πr 2 dr .
0
0
Po scałkowaniu otrzymujemy, że
C=
Podstawiając wzór 12.11
1
12.11
πa 3
do 12.10 otrzymamy znormalizowaną funkcję falową,
odpowiadającą stanowi 1s elektronu w atomie wodoru:
1
ψ 100 ( r ) =
πa
3
e− r / a .
12.12
Prawdopodobieństwo znalezienia elektronu w elemencie objętości dV jest równe
2
2
dW = ψ dV = ψ 4πr 2 dr .
Podstawiając do tego wzoru funkcję falową 12.12 otrzymamy
Wykłady z fizyki – Piotr Posmykiewicz
dW =
8
1 − 2r / a
e
4πr 2 dr .
πa 3
Znajdźmy te odległości rmax od jądra, w których elektron może być znaleziony z
największym prawdopodobieństwem. Badając wyrażenie dW/dr określające maksimum,
otrzymamy, że rmax = a. W rezultacie elektron jest znajdowany z największym
prawdopodobieństwem w odległościach odpowiadających promieniowi Bohra. Wydawało by
się więc, że podejście kwantowo-mechaniczne daje całkowitą zgodność z teorią Bohra.
Jednak, zgodnie z teorią Bohra prawdopodobieństwo (Wkl) znalezienia elektronu w stanie 1s
jest różna od zera tylko dla r = a, gdy tymczasem, zgodnie z mechaniką kwantową (Wkw) w
odległości r = a, prawdopodobieństwo osiąga tylko wartość maksymalną, a pozostałej
przestrzeni jest różna od zera (Rysunek 12.4). W ten sposób, w stanie podstawowym atomu
wodoru najbardziej prawdopodobną odległością od jądra jest odległość równa promieniowi
Bohra. Na tym polega sens kwantowo-mechaniczny promienia Bohra.
Wkl(r)
Wkw(r)
Rysunek 12.4
12.3 Spin elektronu. Spinowa liczba kwantowa.
O.Stern i W.Gerlach przeprowadzając bezpośrednie pomiary momentów magnetycznych,
odkryli (1922) rozszczepienie wąskiej wiązki atomów wodoru, które wiadomo, iż znajdowały
się w stanie s pod działaniem niejednorodnego pola magnetycznego na dwie oddzielne wiązki
atomów. Wstanie s moment pędu elektronu jest równy zero. Moment magnetyczny atomu,
związany z orbitalnym ruchem elektronu jest proporcjonalny do momentu mechanicznego,
dlatego jest on równy zeru i pole magnetyczne nie powinno wpływać na ruch atomów wodoru
w stanie podstawowym, tzn. nie powinno się obserwować żadnego rozszczepienia. Jednak po
zastosowaniu czułych spektroskopów udowodniono, że linie widmowe wodoru wykazują
subtelną strukturę (są dubletami) nawet jeżeli nie ma pola magnetycznego.
Wykłady z fizyki – Piotr Posmykiewicz
9
W celu wyjaśnienia takiej struktury linii widmowych, a także szeregu innych trudności
pojawiających się w fizyce atomowej fizycy amerykańscy S. Goudsmit i G. Uhlenbeck w
1925 roku wysunęli hipotezę, że elektron posiada swój własny niezniszczalny moment
pędu, nie związany z ruchem elektronu w przestrzeni – spin.
Spin elektronu (i wszystkich pozostałych mikrocząstek) jest wielkością kwantową i nie ma
odpowiednika klasycznego; jest to nieodłączna wewnętrzna własność elektronu, podobnie jak
jego masa czy ładunek. Posiadanie przez elektron spinu wynika z otrzymanego przez P.
Diraca relatywistycznego, kwantowego równania dla elektronu.
Jeżeli elektronowi przypisuje się własny mechaniczny moment pędu (spin) Ls, to
związany jest z nim pewien własny moment magnetyczny pms. Zgodnie z ogólnymi
wnioskami mechaniki kwantowej spin jest skwantowany zgodnie z równaniem
Ls =  s( s + 1) ,
gdzie s – spinowa liczba kwantowa.
Analogicznie do orbitalnego momentu pędu, rzut Lsz jest skwantowany tak, że wektor Ls
może przyjmować 2s + 1 orientacji. Ponieważ w doświadczeniach Sterna i Gerlacha były
obserwowane tylko dwie orientacje, to 2s + 1 = 2, skąd s =
1
. Rzut spinu na kierunek
2
zewnętrznego pola magnetycznego jest wielkością kwantową, określoną wielkością
analogiczną do 12.6:
Lsz = m s
gdzie ms – magnetyczna spinowa liczba kwantowa; może przybierać tylko wartości: m s = ±
1
2
.
W ten sposób dane doświadczalne doprowadziły do konieczności scharakteryzowania
elektronów (i ogólnie mikrocząstek) poprzez dodatkowy wewnętrzny stopień swobody.
Dlatego też w celu pełnego opisania stanu elektronu w atomie należy obok głównej, orbitalnej
i magnetycznej liczby podawać dodatkowo magnetyczną spinową liczbę kwantową.
12.4 Zasada nierozróżnialności identycznych cząstek. Fermiony i bozony.
Wykłady z fizyki – Piotr Posmykiewicz
10
Jeżeli przejść od rozpatrzenia ruchu jednej cząstki (jednego elektronu) do układów
wieloelektronowych, to pojawiają się dodatkowe własności, nie mające odpowiednika w
fizyce klasycznej. Niech kwantowo-mechaniczny układ składa się z jednakowych cząstek, na
przykład elektronów. Wszystkie elektrony mają jednakowe własności fizyczne – masę,
ładunek elektryczny, spin i inne wewnętrzne własności (np. liczby kwantowe). Takie cząstki
nazywamy identycznymi.
Nietypowe własności jednakowych identycznych cząstek przejawiają się w podstawowej
zasadzie mechaniki kwantowej – zasadzie nierozróżnialności cząstek identycznych,
zgodnie z którą niemożliwe jest eksperymentalne rozróżnienie cząstek identycznych.
W mechanice klasycznej nawet jednakowe cząstki w zasadzie dają się rozróżnić ze
względu na położenie i pęd. Jeżeli cząstki w jakiejś chwili czasu ponumerować, to w
następnych chwilach można prześledzić tor poruszania się dowolnej z nich. Cząstki
klasyczne, w ten sposób, posiadają indywidualność, dlatego też mechanika klasyczna układów
złożonych z jednakowych cząstek nie różni się od mechaniki klasycznej układów
składających się z różnych cząstek.
W mechanice kwantowej sytuacja jest inna. Ze związków nieoznaczoności wynika, że dla
mikrocząstek w ogóle nie pasuje pojęcie trajektorii; stan cząstki opisywany jest funkcją
2
falową, pozwalającą wyliczyć tylko prawdopodobieństwo ( ψ ) znalezienia mikrocząstki w
okolicach jakiegoś punktu przestrzeni. Jeżeli jednak dwie funkcje falowe identycznych
cząstek pokrywają się w przestrzeni, to decydowanie jaka cząstka znajduje w danej okolicy
pozbawiona jest zupełnie sensu: można jedynie mówić o prawdopodobieństwie znajdowania
się w danym obszarze jednej z cząstek identycznych. W ten sposób w mechanice kwantowej
cząstki identyczne całkowicie tracą swoją indywidualność i stają się nierozróżnialnymi.
2
Uwzględniając sens fizyczny ψ , zasadę nierozróżnialności cząstek identycznych można
zapisać w postaci
ψ ( x1 , x 2 ) = ψ ( x 2 , x 1 ) ,
2
2
12.13
gdzie x1, i x2 – odpowiednio zbiór przestrzennych i spinowych współrzędnych pierwszej i
drugiej cząstki. Z równania 12.13 wynika, że możliwe są dwa przypadki:
ψ ( x1 , x 2 ) = ±ψ ( x 2 , x1 ) ,
Wykłady z fizyki – Piotr Posmykiewicz
11
tzn. zasada nierozróżnialności identycznych cząstek prowadzi do określonej symetrii funkcji
falowych. Jeżeli podczas zamiany miejscami cząstek funkcja falowa nie zmienia znaku, to
nazywa się symetryczną, jeżeli zmienia znak – asymetryczną. Zmiana znaku funkcji falowej
nie oznacza zmiany stanu, ponieważ sens fizyczny i tak posiada tylko kwadrat modułu funkcji
falowej. W mechanice kwantowej udowadnia się, że charakter symetrii nie zmienia się z
czasem. Jest to dowodem na to, że własność symetrii czy antysymetrii jest cechą danego typu
mikrocząstek.
Doświadczenie pokazuje, że symetria lub asymetria funkcji falowych jest określona
poprzez spin cząstek. W zależności od charakteru symetrii wszystkie cząstki elementarne i
utworzone z nich układy (atomy, cząsteczki) dzielą się na dwa typy. Cząstki ze spinem
połówkowym (np. elektrony, protony, neutrony) są opisane antysymetryczną funkcją falową i
podlegają rozkładowi Fermiego-Diraca; cząstki te nazywają się fermionami. Cząstki ze
spinem całkowitym lub połówkowym (np. mezony π, lub fotony) opisywane symetrycznymi
funkcjami falowymi podlegają rozkładowi Bosego-Einsteina i nazywają się bozonami.
Cząstki złożone (np. jądra atomowe) złożone z nieparzystej ilości identycznych fermionów są
fermionami (całkowity spin jest połówkowy), a z parzystej ilości fermionów są bozonami
(całkowity spin jest liczbą całkowitą).
Zależność charakteru symetrii funkcji falowych układu cząstek identycznych w zależności
od spinu cząstek została teoretycznie uzasadniona przez szwajcarskiego fizyka W. Pauliego,
co było jeszcze jednym dowodem na to, że spin jest podstawową charakterystyczną cechą
mikrocząstek.
12.5 Zakaz Pauliego. Rozmieszczenie elektronów w atomie.
Jeżeli identyczne cząstki mają jednakowe liczby kwantowe, to ich funkcja falowa jest
symetryczna względem przestawienia cząstek. Stąd wynika, że dwa jednakowe fermiony,
wchodzące w skład jednego układu nie mogą znajdować się w jednakowym stanie, ponieważ
fermiony powinny mieć funkcję falową antysymetryczną. Uogólniając dane doświadczalne W.
Pauli sformułował zasadę, zgodnie z którym w naturze spotyka się układy fermionów tylko w
stanach, opisywanych antysymetrycznymi funkcjami falowymi (sformułowanie kwantowomechaniczne zakazu Pauliego).
Z podanego twierdzenia wynika podstawowe sformułowanie zasady Pauliego, która
została wprowadzona przez niego do teorii kwantowej jeszcze przed stworzeniem mechaniki
Wykłady z fizyki – Piotr Posmykiewicz
12
kwantowej: w układzie jednakowych fermionów dowolne dwa z nich nie mogą jednocześnie
znajdować się w jednym i tym samym stanie. Należy zwrócić uwagę, że ilość jednakowych
bozonów znajdujących się w tym samym stanie nie jest ograniczone.
Przypomnijmy, że stan elektronu w atomie jednoznacznie jest określony poprzez podanie
czterech liczb kwantowych:
głównej
n
(n = 1, 2, 3, ...),
orbitalnej
l
(l = 0, 1, 2,...n - 1),
magnetycznej
ml
(ml = -l, ...-1, 0, +1,...+l),
spinowej
ms
1 1
(ms = + , − ).
2 2
Rozkład elektronów w atomie podlega zakazowi Pauliego, który w tym wypadku może
być zastosowany w swoim najprostszym sformułowaniu: w jednym i tym samym atomie nie
może znajdować się więcej niż jeden elektron z jednakowym zestawem czterech liczb
kwantowych n, l, ml, ms tzn.
Z(n, l, ml, ms) = 0 lub 1
Gdzie Z(n, l, ml, ms) – ilość elektronów znajdujących się w stanie kwantowym opisanym
przez zestaw czterech liczb kwantowych n, l, ml, ms. W rezultacie zakaz Pauliego stwierdza,
że dwa elektrony, związane z danym atomem, muszą różnić się wartością co najmniej jednej
liczby kwantowej.
Zgodnie ze wzorem 12.8 danemu n odpowiada n2 różnych stanów różniących się
(
)
wartościami l i ml. Liczba kwantowa ms może przyjmować tylko dwie wartości ± 1 2 .
Dlatego Z(n) – maksymalna liczba elektronów, znajdujących się w stanach określonych daną
główną liczbą kwantową n jest równa 2n2, ponieważ
n−1
Z ( n) = ∑ 2( 2l + 1) = 2 n .
l =0
2
Wykłady z fizyki – Piotr Posmykiewicz
13
Zbiór elektronów w atomie wielo-elektronowym, posiadający daną liczbę kwantową
tworzy powłokę elektronową. W każdej z powłok elektrony podzielone są na podpowłoki
odpowiadające danemu l. Ponieważ orbitalna liczba kwantowa przyjmuje wartości od 0 do n –
1, to liczba podpowłok jest równa numerowi porządkowemu n-tej powłoki. Ilość elektronów
w podpowłoce jest określone magnetycznymi i spinowymi liczbami kwantowymi:
maksymalna ilość elektronów z danym l jest równa 2(2l + 1). Oznaczenia powłok, jak
również rozkład elektronów w powłokach i podpowłokach jest przedstawione w tabeli:
Główna liczba kwantowa n
1
2
3
4
5
Symbol powłoki
K
L
M
N
O
Maksymalna liczba elektronów
2
8
18
32
50
w powłoce
Orbitalna liczba kwantowa l
0 0 1 0 1 2 0 1 2 3 0 1 2 3 4
Symbol podpowłoki
1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f 5g
Maksymalna liczba elektronów
2 2 6 2 6 10 2 6 10 14 2 6 10 14 18
w podpowłoce
Pierwiaste
k
12.6 Układ okresowy pierwiastków Mendelejewa .
Okres
Zakaz Pauliego, który stanowi podstawę systematyki zapełniania stanów elektronowych
w atomie; pozwala objaśnić okresowy układ pierwiastków Mendelejewa.
Wykłady z fizyki – Piotr Posmykiewicz
14
Ponieważ własności chemiczne i niektóre
własności
fizyczne
zewnętrznych
pierwiastków
(elektronów
zależą
od
walencyjnych),
to
okresowość własności chemicznych pierwiastków
powinna być związana z określoną okresowością
rozkładu elektronów w atomach. Dlatego też, aby
objaśnić tablicę Mendelejewa będziemy zakładać,
że
każdy
następny
pierwiastek
powstaje
z
poprzedniego poprzez dodanie do jądra jednego
protonu i odpowiednio jednego elektronu do
powłoki
elektronowej
atomu.
Zaniedbamy
oddziaływanie elektronów między sobą, wnosząc,
tam gdzie jest to konieczne odpowiednie poprawki.
Atomy
pierwiastków
chemicznych
będziemy
rozpatrywać w ich podstawowym stanie.
Jedyny elektron wodoru znajduje się w stanie
1s, scharakteryzowanym liczbami kwantowymi n =
1, l = 0, ml = 0, ms = ± 1 / 2 (kierunek jego spinu
jest dowolny). Obydwa elektrony atomu He
znajdują si w stanie 1s, ale mają antyrównoległe
orientacje
spinów.
Konfiguracja
elektronowa
atomu He jest zapisywana w postaci 1s2 (dwa
elektrony 1s). Na atomie helu ulega zakończenie
zapełnianie
zakończeniu
K-tej
I
powłoki,
okresu
co
układu
odpowiada
okresowego
pierwiastków (patrz tablica poniżej).
Trzeci elektron Li (Z = 3), zgodnie z zakazem Pauliego, nie może już znajdować się
całkowicie zapełnionej K-tej powłoce i zajmuje najniższy energetycznie stan z n = 2 (powłoka
L), tzn. stan 2s. Konfiguracja elektronowa litu ma postać 1s22s. Atom Li rozpoczyna II okres
układu okresowego pierwiastków. Czwarty elektron Be (Z = 4) kończy zapełnianie
podpowłoki 2s. W następnych sześciu pierwiastkach od B (Z = 5) do Ne (Z = 10) następuje
stopniowe zapełnianie podpowłoki 2p. II okres układu okresowego kończy się na neonie –
neutralnym gazie, w którym podpowłoka 2p jest całkowicie zapełniona.
Wykłady z fizyki – Piotr Posmykiewicz
15
Jedenasty elektron Na (Z = 11) znajduje się w powłoce M (n = 3) i zajmuje najniższy stan
3s. Konfiguracja elektronowa posiada postać 1s22s22p63s. Elektron 3s jest elektronem
walencyjnym (tak jak elektron 2p w Li), dlatego własności optyczne Na są zbliżone do
własności Li. Ar (Z = 18) ma własności podobne do He, Ne: w jego zewnętrznej powłoce
wszystkie stany s i p są zapełnione. Ar jest obojętnym chemicznie gazem i zamyka III okres
układu pierwiastków.
Dziewiętnasty elektron K (Z = 19) powinien zajmować stan 3d w powłoce M. Jednak
zarówno chemicznie jak i fizycznie atom K jest podobny do atomów Li i Na, które posiadają
zewnętrzny elektron walencyjny w stanie s. Dlatego też, 19-ty elektron walencyjny potasu
także powinien znajdować się w stanie s, jednak może to być tylko stan nowej powłoki
(powłoki N). Oznacza to, że zapełnianie powłoki N dla K zaczyna się przy nie zapełnionej do
końca powłoce M. Oznacz to, że w rezultacie oddziaływań elektronów między sobą stan n =
4,
l = 0 posiada mniejszą energię niż stan n = 3, l = 2. Własności spektroskopowe i
chemiczne Ca (Z = 20) pokazują, że jego 20-ty elektron znajduje się również w stanie 4s
powłoki N. W następnych pierwiastkach następuje zapełnianie powłoki M (od Sc (Z = 21) do
Zn (Z = 30)). Dalej powłoka N jest zapełniana do Kr (Z = 36), który tak samo jak poprzednio
Ne i Ar, ma zapełnione całkowicie stany s i p zewnętrznej powłoki. Na kryptonie kończy się
IV okres układu okresowego pierwiastków.
Podobną analizę można zastosować do pozostałych pierwiastków układu Mendelejewa.
Zwróćmy jedynie uwagę, że początkowe pierwiastki następnych okresów Rb, Cs, Fr również
są pierwiastkami alkalicznymi. Oprócz tego atomy gazów obojętnych (He, Ne, Ar, Kr, Xe,
Rn) zajmują w tablicy oddzielne położenie – w każdym z nich stany s i p powłoki zewnętrznej
są całkowicie zapełnione i na nich kończą się kolejne okresy układu okresowego.
Każdą z dwu grup pierwiastków – lantanowce (od lantanu (Z = 57) do lutetu (Z = 71)) i
aktynowce (od aktynu (Z = 89) do lorensa (Z = 103)) – należy umieszczać w dwóch
komórkach układu okresowego, ponieważ własności chemiczne w obrębie jednej grupy są
bardzo zbliżone. Wynika to z tego, iż dla lantanowców wypełnianie podpowłoki 4f, która
może zawierać 14 elektronów, zaczyna się dopiero po tym w całości zostaną zapełnione
podpowłoki 5s, 5p, i 6s. Dlatego też, dla tych pierwiastków zewnętrzna powłoka P (6s2) jest
jednakowa. Analogicznie dla aktynowców, powłoka Q (7s2) jest taka sama.
W ten sposób, odkryta przez Mendelejewa okresowość własności chemicznych
pierwiastków, daje się wyjaśnić powtarzalnością struktury zewnętrznych powłok pokrewnych
pierwiastków. Tak więc, gazy obojętne mają jednakowe zewnętrzne powłoki składające się z
8 elektronów; w zewnętrznej powłoce metali alkalicznych (Li, Na, K, Rb, Cs, Fr) znajduje się
Wykłady z fizyki – Piotr Posmykiewicz
16
tylko jeden elektron s; w zewnętrznej powłoce metali ziem alkalicznych (Mg, Ca, Sr, Ba, Ra)
znajdują się dwa elektrony s; gadoliny (F, Cl, Br, I, At) mają powłoki, w których brakuje
jednego elektronu do pełnego zapełnienia powłoki tak jak w gazach obojętnych.